By guest contributor Guy Cameron, Founding Director, Cameron Hume Limited
Tetris, the addictive computer game where falling tetrominoes must be lined up to fill the available space, was invented in 1984. Despite there being many more sophisticated games available today, it remains popular because, like all good games, Tetris has a clear objective with simple rules and is difficult to master. In 2003 mathematicians from MIT revealed that the reason Tetris is so challenging is that it belongs to a class of problems beloved by cryptologists. Cryptologists study codes and a good code is one that is easy to unlock if you have the key, but where the task of finding that key is hard. For a cryptologist a hard task is one that takes a long time to complete.
Cash flow matching has features in common with Tetris: it is one of the oldest techniques for matching assets to liabilities; the objective of cash flow matching is clear, but finding a perfect solution is very difficult; and despite more sophisticated approaches being available it remains popular.

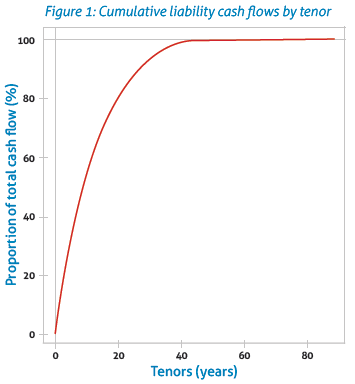
Cash flow matching involves putting together a portfolio of bonds with cash flow receipts that match the timing and scale of expected cash flow payments. Figure 1 is an example of the distribution of cash flows that a matching portfolio would seek to replicate. The graph shows the proportion of cash flows payable by an annuity provider within a certain time period: in this example, the final cash flow is in 90 years. A cash flow matching portfolio would consist of bonds that together have cash flows distributed similarly. While approximate matches are achievable, exact matches are hard to find.
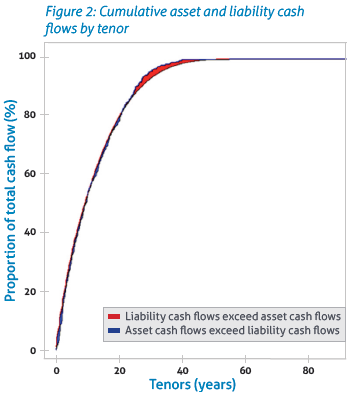
In Figure 2 we have added the cash flows from a portfolio that approximately matches those of Figure 1. The shaded areas represent the gap between the asset and liability cash flows. The small blue shaded area around 10 years illustrates that in this section of the curve the asset cash flows exceed those of the liabilities – the asset curve bulges through the liability curve. At tenors greater than 20 years the situation reverses and the asset curve fails to reach the liability curve. In this example, the value of the assets is equal to that of the liabilities.
This is a relatively good match, but it is not perfect and achieving perfection is hard in the sense meant by cryptologists. The liability curve consists of about one thousand cash flows and to match each of those exactly would be a laborious task, even if practical. Like Tetris, we have to find bonds with the right shape of cash flows to fill the gaps.

